【Python】ランダムな数値の生成方法（randomモジュールの使い方）

Python標準ライブラリのrandomモジュールは、

整数値をある範囲から一様に抽出する関数
実数値を統計学に出てくる様々な分布（一様分布や正規分布、ガウス分布など）に基づいて生成する関数

がサポートされており、場面に応じて適切な関数を使うことができます。
本記事では、randomモジュールを使ってランダムな数値を生成する方法について解説します。

整数のランダム値を生成
1. random.randrange() の使いかた
2. random.randint() の使いかた
乱数の初期化（seed）
1. seed()の引数を固定
2. seed()の引数を省略
実数のランダム値を生成
「擬似」乱数について
今回確認した環境
まとめ

整数のランダム値を生成

ランダムな整数値を生成する関数は下記2つあります。

random.range()
random.randint()

それぞれ具体例を交えて下記に記載します。
尚、randomモジュールは標準ライブラリなので、新たにインストールする必要はありません。

random.randrange() の使いかた

基本の書式は以下です。

random.randrange(start, stop[, step])

startからstop – 1までの整数値からランダムに選ばれた値を返します。

この関数はrange(start, stop, step) で生成されるイテラブルからランダムに抽出された要素を返しています。よって、引数（start、stop、step）は、range()と同じです。

具体例を以下に示します。最初にrandaomモジュールをインポートします。

stop引数のみ

# randomモジュールをインポート
>>> import random

# 0〜9でランダムな整数値を出力
>>> random.randrange(10)
7

# （参考）range()で生成される要素
>>> list(range(10))
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

start, stop引数のみ

# 1〜9でランダムな整数値を出力
>>> random.randrange(1, 10)
7

# （参考）range()で生成される要素
>>> list(range(1, 10))
[1, 2, 3, 4, 5, 6, 7, 8, 9]

start, stop、step引数の場合

# 1〜19の間で2stepの整数群からランダムに整数を出力
>>> random.randrange(1, 20, 2)
11

# （参考）range()で生成される要素
>>> list(range(1, 20, 2))
[1, 3, 5, 7, 9, 11, 13, 15, 17, 19]

何回か同じ処理を繰り返すと、毎回異なる値が出力されます。（なぜ毎回異なる値になるかは後述）

>>> random.randrange(10, 50, 2)
12
>>> random.randrange(10, 50, 2)
10
>>> random.randrange(10, 50, 2)
28

参考）Python公式リファレンス：random.randrange()

random.randint() の使いかた

基本の書式は以下です。

random.randint(a, b)

引数で指定したa〜bの範囲のランダムな整数値を返します。
randrange(a, b+1)と同じで、これよりも直感的に分かりやすいですね。

以下は10から100の間からランダムに整数値を一つ取得する例です。何回か繰り返すと異なる値を返すのはrandrange()と同様です。

>>> import random
>>> random.randint(10, 100)
63
>>> random.randint(10, 100)
15
>>> random.randint(10, 100)
18

参考）Python公式リファレンス：random.randint()

乱数の初期化（seed）

乱数を初期化するには、random.seed()を使います。

引数を省略するとシステム時刻が設定され、毎回異なる値が生成されます。
引数を任意の数値に固定すると、毎回同じ値が生成されます。

例を以下に示します。random.seed()の引数の有無の影響も併せて確認する為、初期化→ランダム値生成を５回繰り返してみました。

seed()の引数を固定

引数を、例えば10に設定してみました。初期化した後はランダムな数値が生成されますが、同じseed値で初期化をすると、同じ値が毎回同じ値が生成されます。

#0〜100の整数値をランダムに生成。これを５回繰り返す
>>> for i in range(5):
...     random.seed(10)
...     random.randint(0, 100)
... 
73
73
73
73
73

seed()の引数を省略

この場合は上述の通り、毎回異なる値が出力されます。

#0〜100の整数値をランダムに生成。これを５回繰り返す
>>> for i in range(5):
...     random.seed()
...     random.randint(0, 100)
... 
79
59
33
86
51

実数のランダム値を生成

一様分布や正規分布、ガウス分布など統計学に出てくる様々な実数値分布に基づいて、ランダムな浮動小数点数を生成できます。

random.random()

randomモジュールで対応している関数の基礎となる関数です。
引数はとらず、0.0〜1.0の間のランダムな浮動小数点数を返します。

具体例は以下です。

>>> import random
# ［0.0,1.0]の実数値
>>> random.random()
0.45502898782149415

>>> random.random()
0.08139912660907467

>>> random.random()
0.24940586447758728

この関数でランダム値を1000個生成してヒストグラムにプロットしてみました。
分布の様子が解ると思います。（コードはこちら）

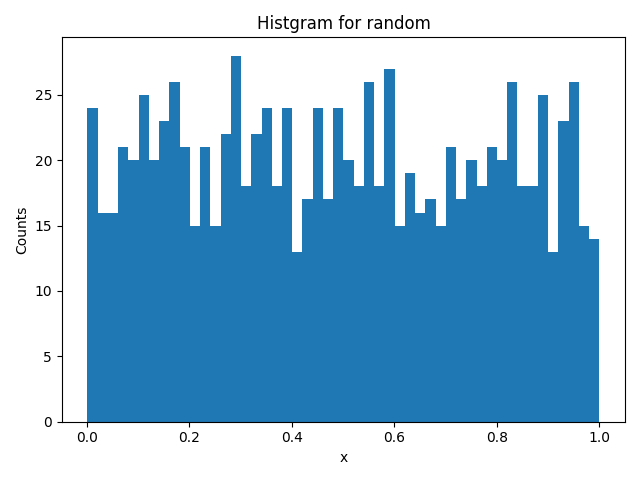
参考）Python公式リファレンス：random.random()

一様分布：random.uniform()

使い方は以下です。

random.uniform(a, b)

引数に設定したaとbの間の浮動小数点数を返します。
（a ≦ bの場合は　a ≦ N ≦ b、b ≦ aの場合は　b ≦ N ≦ a）

具体例を示します。

>>> import random
#[10.0, 20.0]の実数値
>>> random.uniform(10, 20)
12.210699423563693

>>> random.uniform(10, 20)
17.554472321996638

>>> random.uniform(10, 20)
12.906732949515154

この関数でランダム値を1000個生成して分布をプロットしました。（コードは上記と同じ）

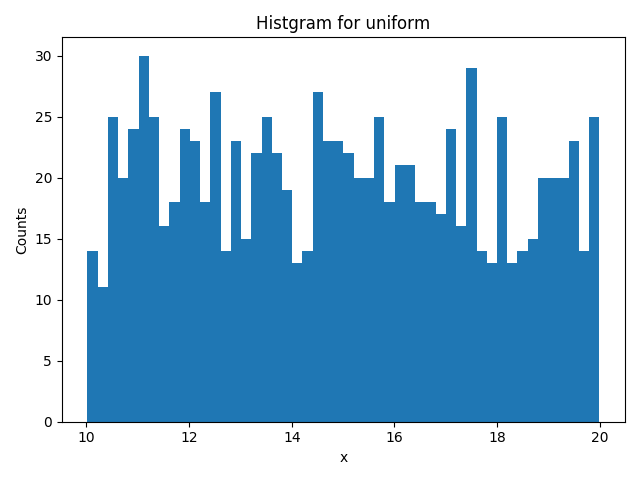
参考）Python公式リファレンス：random.uniform()

正規分布：random.normalvariate()

よく出てくる正規分布です。関数の使いかたは以下です。

random.normalvariate(mu, sigma)

mu：平均、sigma：標準偏差を引数にとります。

具体例を示します。

>>> import random

# 正規分布（mu = 1, sigma = 0.2) 
>>> random.normalvariate(1, 0.2)
1.0224198012476196

>>> random.normalvariate(1, 0.2)
0.7581639461744528

>>> random.normalvariate(1, 0.2)
1.2633150295500526

この関数でランダム値を1000個生成して分布をプロットしました。正規分布の関数曲線も重ねました。（コードは上記と同じ）

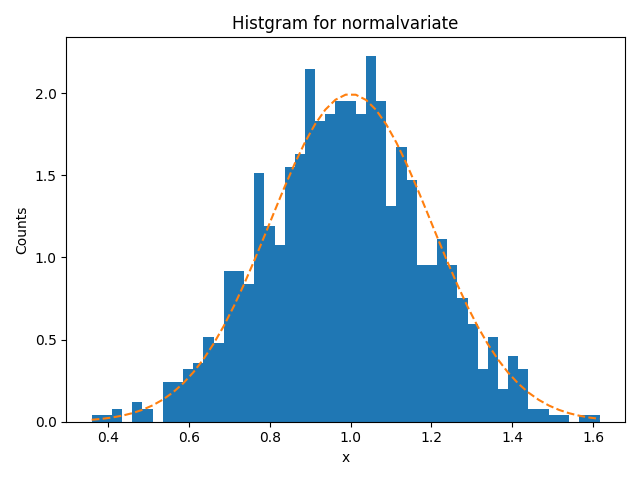
参考）Python公式リファレンス：random.normalvariate()

その他の実数分布

その他の関数を用いた実数分布について紹介します。
（個人的に）かなりマニアックだと思うので、ここではそれぞれの関数で生成したランダム値1000個の分布を記載します。尚、それぞれの関数のパラメータは適当に決めました。（コードは上記と同じ）

三角分布：random.triangular(low, high, mode)

例）low = 0, high = 1, mode = 0.5 (両境界の中点）

>>> random.triangular(0, 1)
0.22094246737199522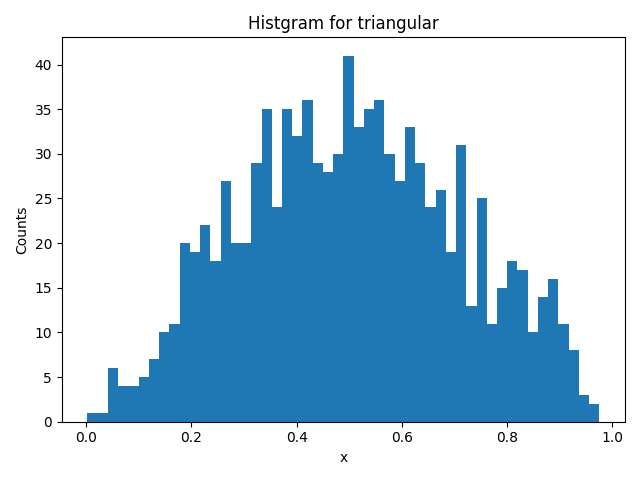

ベータ分布：random.betavariate(alpha, beta)

例）alpha = 4, beta = 7

>>> random.betavariate(4, 7)
0.4236194633930723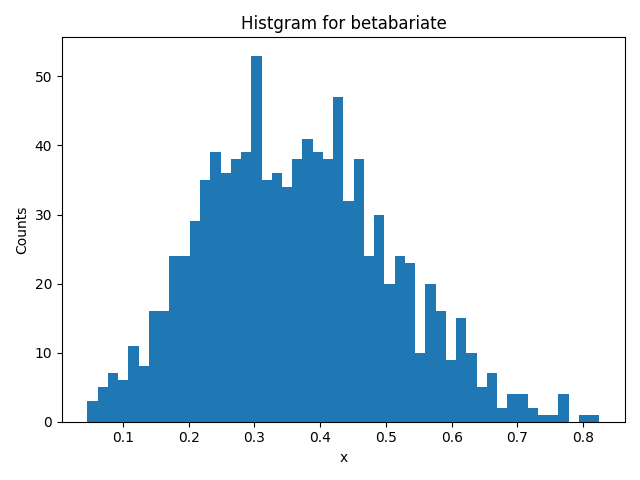

指数分布：random.expovariate(lambd)

例）lambd = 1/0.5 (平均にしたい値の逆数）

>>> random.expovariate(1/0.5)
0.45753238788344547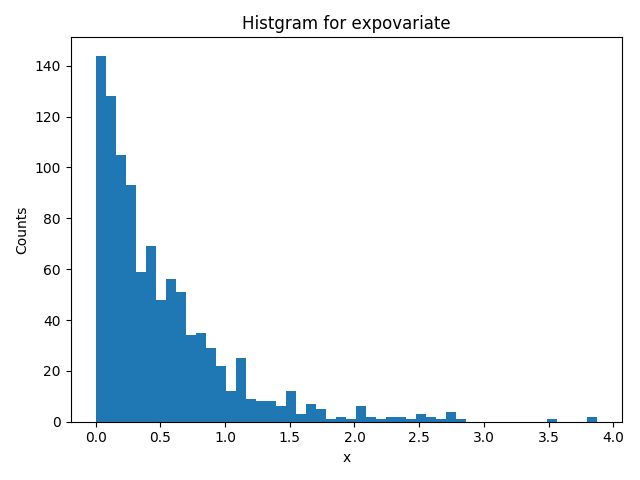

ガンマ分布：random.gammavariate(alpha, beta)

例）alpha = 4, beta = 7

>>> random.gammavariate(4, 7)
19.10787433161909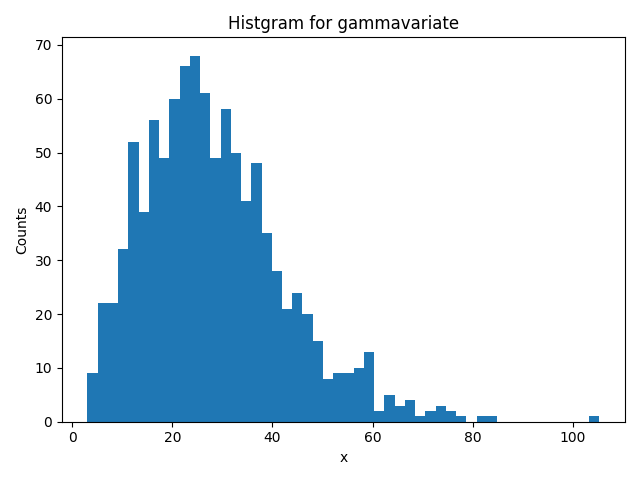

ガウス分布：random.gauss(mu, sigma)

例）mu = 1, sigma = 0.2

>>> random.gauss(1, 0.2)
0.5367721409710682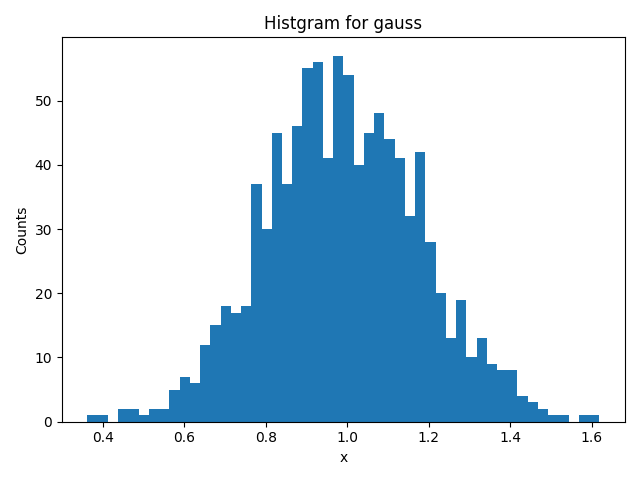

対数正規分布：random.lognormvariate(mu, sigma)

例）mu = 1, sigma = 0.2 （下図の横軸は自然対数ln(x)に変換）

>>> random.lognormvariate(1, 0.2)
2.833637697234802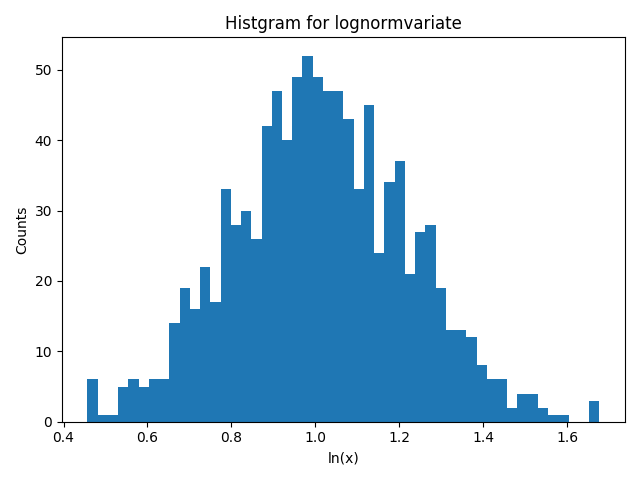

フォン・ミーゼス分布：random.vonmisesvariate(mu, kappa)

例）mu = pi/2, kappa = 5

>>> random.vonmisesvariate(math.pi/2, 5)
1.6906121883985528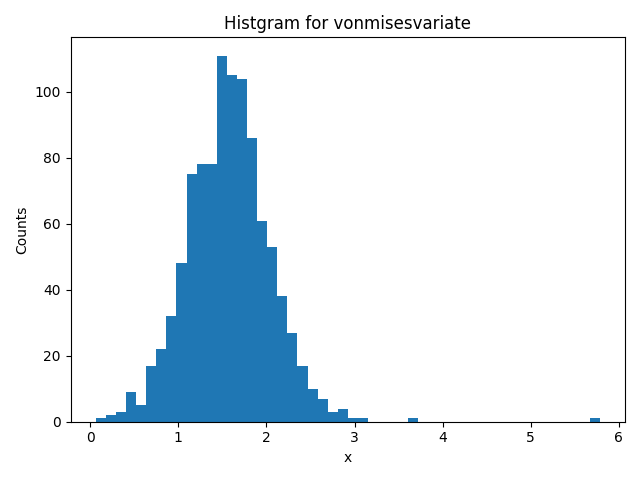

パレート分布：random.paretovariate(alpha)

例）alpha = 100

>>> random.paretovariate(100)
1.0131729401420186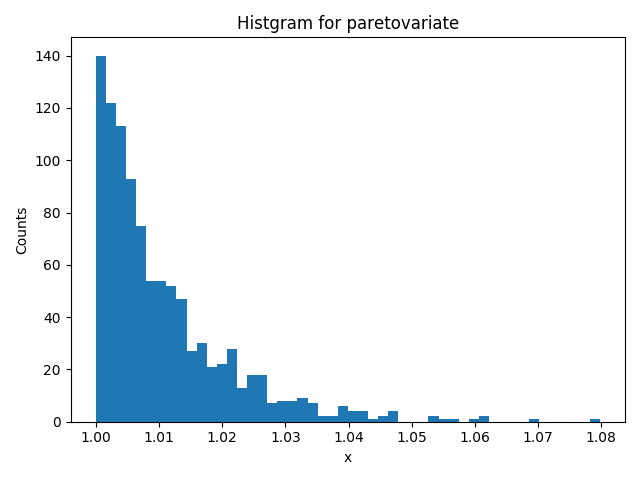

ワイブル分布：random.weibullvariate(alpha, beta)

例）alpha = 4, beta = 2

>>> random.weibullvariate(4, 2)
2.1536509784397295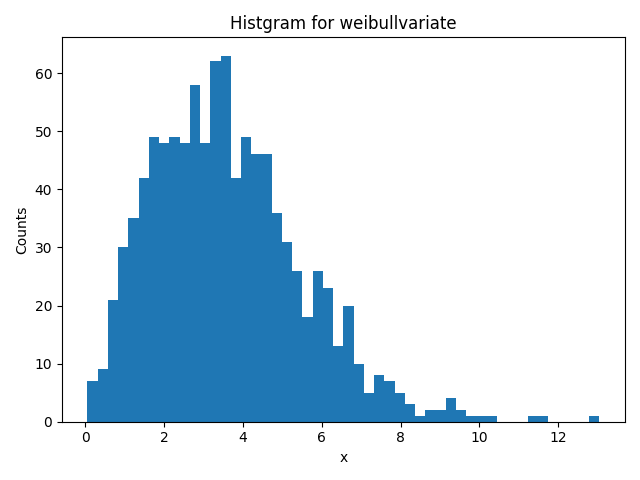

「擬似」乱数について

最後に、なぜ「疑似」乱数なのか？について触れておきます。
下記にあるとおり、計算機で確率的な計算によって乱数を求めているので「擬似」乱数とのこと。ちなみにPythonでは中心となる乱数生成器としてメルセンヌツイスタというものを使っています。

擬似乱数（ぎじらんすう、pseudorandom numbers）は、乱数列のように見えるが、実際には確定的な計算によって求めている擬似乱数列による乱数。
（中略）
真の乱数列は本来、規則性も再現性もないものであるため、本来は確定的な計算によって求めることはできない（例：サイコロを振る時、今までに出た目から次に出る目を予測するのは不可能）。一方、擬似乱数列は確定的な計算によって作るので、その数列は確定的であるうえ、生成法と内部状態が既知であれば、予測可能でもある。

wikipedia「擬似乱数」