今回は、Pythonの数値演算のうち指数関数・対数関数についてです。それぞれ主に下記の関数を使うことで計算することが出来ます。
- 指数関数:**演算子、pow()、math.pow()
- 対数関数:math.log()
他にも、特定の定数(自然対数eの場合など)に特化した場合の関数もありますので、これらも併せて基本的な使い方について解説します。
また、各関数の例としてmatplotlibを使ったグラフも併せて載せています。
確認した環境
- OS: Ubuntu16.04LTS
- Python3.7.2@Anaconda
定数 \(e\)(自然対数の底)
ネイピア数とも呼ばれます。記号として\(e\)が用いられ、
\(e = 2.71828 18284 59045 23536 02874 71352 …\)
となる無理数です。Pythonではmathモジュールで定義され、math.eで表記できます。
>>> math.e
2.718281828459045指数関数
\(y=a^x\)
この計算をする関数は以下3通りあります。
(1) **演算子
a ** x で \(a\)の\(x\)乗を計算できます。
返り値の型は被演算子のうち最も広い精度の型に合わせられます。
例えば、被演算子がint型とfloat型の場合、返り値はfloat型となります。被演算子が両方共int型の場合は、返り値はint型になります。
例を以下に示します。
# 被演算子が両方ともint型
>>> 2**3
8
# 異なる型の被演算子が混ざっている場合
>>> 2**2.5
5.656854249492381
>>> 2.3**4
27.98409999999999
# マイナスの数値も計算可能(※)
>>> (-2)**4
16
>>> (-2)**3.5
(-4.849353914918763e-15-11.313708498984761j)(※)**演算子は-演算子よりも優先順位が高いので、マイナスの数値を計算する際は演算子の優先順位に注意!です。
# ()を付けない場合の例
>>> -2**4
-16
>>> -2**3.5
-11.313708498984761(2) 組込み関数: pow()
pow(a, x[, z])は\(a\)の\(x\)乗を返します。
引数は数値型をとり、返り値の型は引数のうち最も広い精度の型に合わせられます。
例えば、引数がint型とfloat型の場合、返り値はfloat型となります。引数が両方共int型の場合は、返り値もint型になります。(ここがmathモジュールと異なる点)
例を以下に示します。
# 被演算子が両方ともint型
>>> pow(2, 3)
8
# 異なる型の被演算子が混ざっている場合
>>> pow(2.3, 4)
27.98409999999999
>>> pow(2, 3.5)
11.313708498984761
# マイナスの数値も計算可能
>>> pow(-2, 4)
16
>>> pow(-2, 3.5)
(-4.849353914918763e-15-11.313708498984761j)また、引数が以下の条件を両方満たす場合は、
- a およびx がint型
- x > 0
第三引数zを設定して、\(a\)の\(x\)乗を\(z\)で割った余りを求めることが出来ます。
公式リファレンスによると、pow(a, x) % z より効率よく計算されるとのこと。
# 2の3乗(=8)を4で割った余り
>>> pow(2, 3, 4)
0
# 2の3乗(=8)を3で割った余り
>>> pow(2, 3, 3)
2尚、条件を満たさない場合はTypeErrorを返します。
# 引数が整数型でない場合
>>> pow(2.1, 3, 3)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: pow() 3rd argument not allowed unless all arguments are integers
# 第二引数xが負の場合
>>> pow(2, -3, 2)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: pow() 2nd argument cannot be negative when 3rd argument specified(3) mathモジュール: math.pow()
math.pow(a, x)は\(a\)の\(x\)乗を返します。
この関数は両方の引数(a, x)をfloat型に変換しますので、引数の型に関わらず返り値もfloat型となります。
# 返り値はfloat型
>>> math.pow(2, 3)
8.0
>>> math.pow(2.3, 4)
27.98409999999999
>>> math.pow(2, 3.5)
11.313708498984761
# マイナスの数値も計算可能
>>> math.pow(-2, 4)
16.0
# 但し、結果が複素数(a < 0 且つxが整数でない場合)の場合はTypeErrorを送出
>>> math.pow(-2, 3.5)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: math domain error\(y=\sqrt{x}\)
math.sqrt(x)はxの平方根\(\sqrt{x}\)を返します。返り値はfloat型になります。
>>> import math
>>> math.sqrt(16)
4.0
>>> math.sqrt(2)
1.4142135623730951マイナス値の平方根は実数値として成り立たないのでValueErrorが返ります。
>>> math.sqrt(-2)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: math domain errorちなみに、マイナス値の平方根(虚数)を求めるにはcmathモジュールを使います。
>>> import cmath
>>> cmath.sqrt(-2)
1.4142135623730951jまた、\(\sqrt{x}\) は \(x^\frac{1}{2}\) とかけるので、上述の**演算子やpow()等を使って書くことも出来ます。
この場合はマイナス数値の計算もできているようですが、sqrt()を使ったほうが精度は良さそうです。
>>> 2**0.5
1.4142135623730951
>>> pow(2, 0.5)
1.4142135623730951
>>> math.pow(2, 0.5)
1.4142135623730951
# マイナス数値の平方根も計算はできています
>>> (-2)**0.5
(8.659560562354934e-17+1.4142135623730951j)
>>> pow(-2, 0.5)
(8.659560562354934e-17+1.4142135623730951j)\(y=e^x\)
自然対数の底\(e\)の\(x\)乗は、math.exp(x)を使います。
>>> import math
# int型を入力
>>> math.exp(2)
7.38905609893065
# float型を入力
>>> math.exp(1.2)
3.3201169227365472
# マイナス値も可能
>>> math.exp(-2.5)
0.0820849986238988また、平方根\(\sqrt{x}\) と同様に上述の**演算子やpow()等を使って書くことも出来ます。
但し、公式によると、精度はexp(x)の方良いようです。
>>> import math
>>> math.e ** 2
7.3890560989306495
>>> pow(math.e, 2)
7.3890560989306495
>>> math.pow(math.e, 2)
7.3890560989306495\(y=e^x-1\)
math.expm1(x)で計算できます。
公式によると、小さい浮動小数点\(x\)で最大精度で計算できるそうです。
>>> math.expm1(0)
0.0
>>> math.expm1(1)
1.718281828459045上記の指数関数について、matplotlibを使って簡単なグラフを書いてみました。コードはこちら。
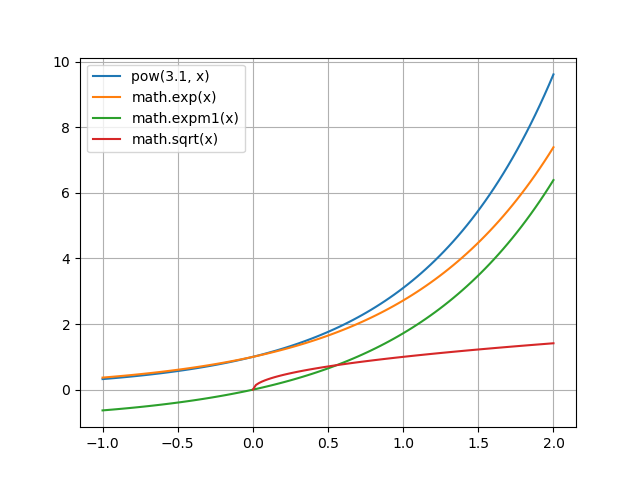
対数関数
\(y=\log_{a}{x}\)
一般的な関数としてはmath.log(x[, a])を使います。
- 引数が1つの場合、xの自然対数\(\ln{x}\)を返します。(対数の底が\(e\))
>>> math.log(1)
0.0
>>> math.log(math.e)
1.0# 2を底とした10の対数
>>> math.log(10, 2)
3.3219280948873626
# 10を底とした2の対数
>>> math.log(2, 10)
0.30102999566398114\(y=\log_2{x}\)
math.log2(x)で計算できます。公式によると、この関数はmath.log(x, 2) よりも正確な値を返すとのこと。(Python3.3以降で追加)
# 底が2であることを確認
>>> math.log2(2)
1.0
# 計算例
>>> math.log2(10)
3.321928094887362
>>> math.log2(2.3)
1.2016338611696504\(y=\log _{10}{x}\)
math.log10(x)で計算できます。公式によると、この関数はmath.log(x, 10) よりも正確な値を返すとのこと。
# 底が10であることを確認
>>> math.log10(10)
1.0
# 計算例
>>> math.log10(2)
0.3010299956639812
>>> math.log10(2.3)
0.36172783601759284\(y=\ln{x+1}\)
math.log1p(x)で計算できます。公式によると、ゼロ近傍のxに対して精度よく計算されるとのこと。
# 底が自然対数eであることを確認
>>> math.log1p(math.e-1)
1.0
# 計算例
>>> math.log1p(2)
1.0986122886681096
>>> math.log1p(10)
2.3978952727983707
>>> math.log1p(2.3)
1.1939224684724346上記の対数関数について、matplotlibを使って簡単にグラフを書いてみました。コードはこちら。
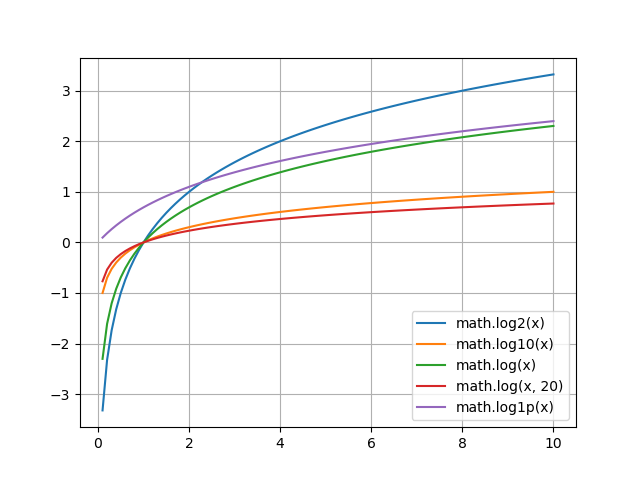
まとめ
今回は、Pythonの数値演算のうち、指数関数・対数関数の計算方法についてまとめました。


コメント
[…] 指数関数と対数関数について | Hbk project […]
[…] 指数関数と対数関数について | Hbk project […]